[4.1]Greedy Algorithms - Analysis
Greedy Algorithm貪婪演算法,指的是「當一演算法 以小步驟 去發展解答,並且 每一步驟都以短淺的眼光選擇當下最好的」,基本上任何問題都很容易發展出一個貪婪演算法,因為通常是以直覺的方式想出來,但是這樣的演算法通常無法產生最佳解(not optimal)。因此,在在貪婪演算法中最困難的部份是要證明該演算法為optimal,通常我們以下面兩種方法來證明:
- The greedy algorithm stays ahead - 該演算法在每一步都維持最佳解
- An exchange argument - 對任何candidate solution,若不是optimal的部分便換掉換成另一種組合
Stays Ahead - Interval Scheduling
Interval Scheduling 是一經典問題。
Given : 一堆附有起始、結束時間的工作集合(set of jobs with start times and finish times)
Goal :找到能達到最多工作且工作不重疊的子集合(find maximum cardinality subset of mutually compatible jobs)
e.g.為機檯安排工作,只有一台機器,要處理愈多工作愈好。如下表,共有i1~i10的時間段(interval)及A~G共7個工作的起始結束時間,要安排最多的工作,解答可以是{A,E,G}
| A | A | A | |||||||
|---|---|---|---|---|---|---|---|---|---|
| B | B | ||||||||
| C | C | C | |||||||
| D | D | D | D | D | |||||
| E | E | E | |||||||
| F | F | F | F | ||||||
| G | G | G | G | ||||||
| i1 | i2 | i3 | i4 | i5 | i6 | i7 | i8 | i9 | i10 |
設計演算法
Greedy Rule : 重複Repeat,直到執行完所有Interval
從i1開始選擇一個工作,一但有工作被接受後,就排除所有與其衝突的工作,例如選A就排除BC。接者選擇下一個interval,直到所有interval都選擇完畢。
接下來另一個重要的事情就是要決定:要選擇哪一個工作,一般我們可以想到下面四種方法
- 找最找開始的
- 找有最短區間的
- 找與其他工作衝突最小的
- 找最找結束的
這就是貪婪演算法的實行過程,我們幾乎可以很快想出幾種演算法,但是困難的地方就是 究竟它們可以給我們最佳解嗎?我們先試著看有沒有反例可以說明該演算法無法得出最佳解。
實心色塊代表我們所選擇的;空心則是因為選擇實心而會被放棄的。
找最找開始的

找有最短區間的
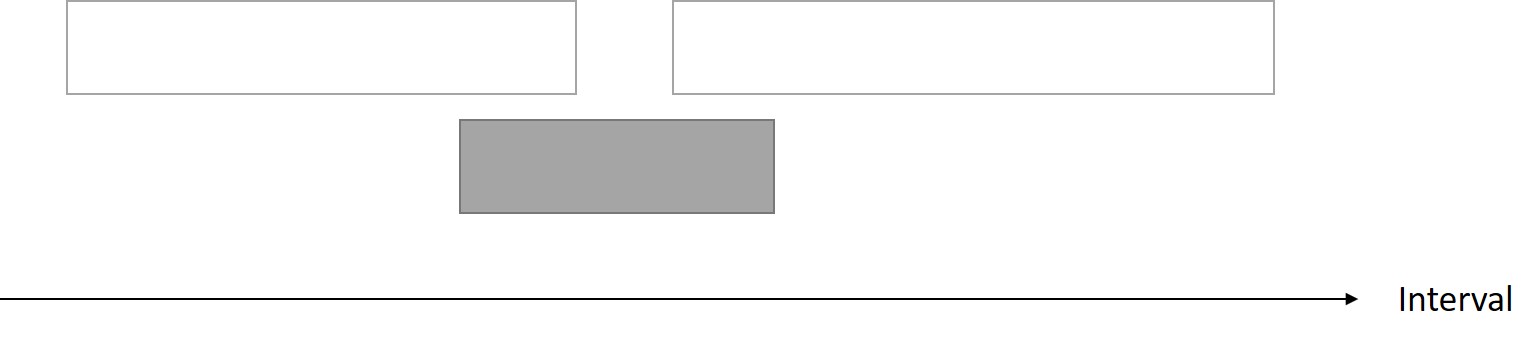
找與其他工作衝突最小的
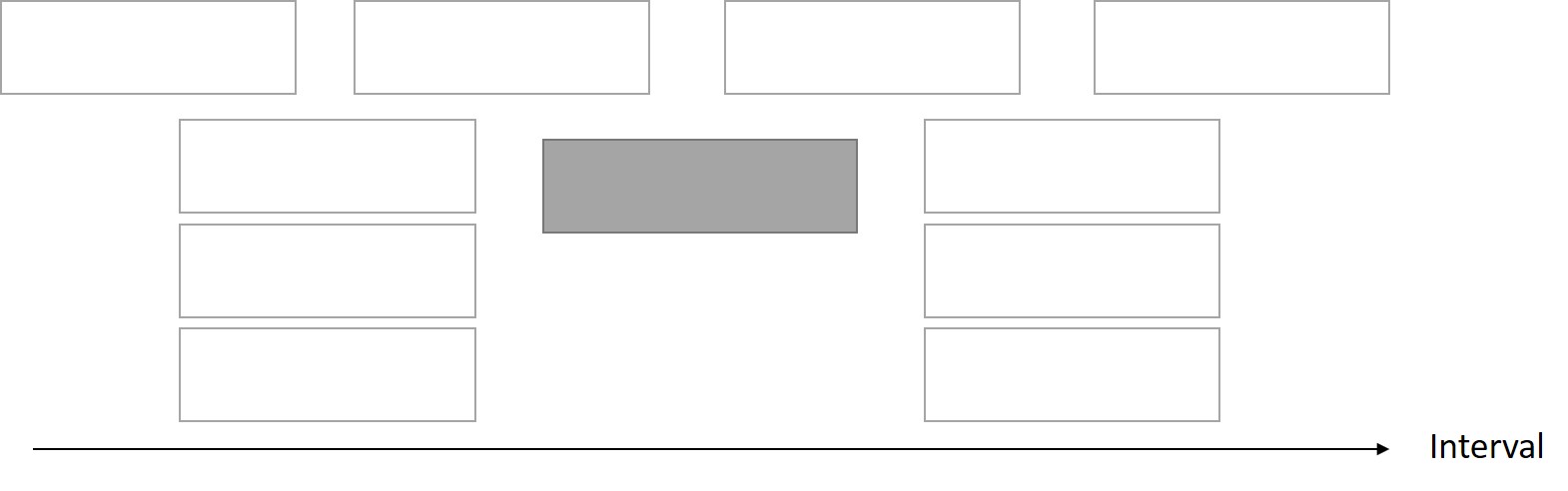
找最找早結束的
對於這一演算法想不到可能違反最佳解的例子,於是我們先將此演算法以Pseudo Code表示,在進一步分析。
Pseudo Code
Initially let R be the set of all requests, and let the set of accepted requests A be empty
While R is not yet empty
Choose a request i∈R that has the smallest finishing time
Add request i to A
Delete all requests from R that are not compatible with request i
EndWhile
Return the set A as the set of accepted requests

分析演算法
首先對於我們得到的被接受的要求集合A,
定理1
A是一相容解集合
接下來要一步步證明此演算法是optimal,我們假設此問題存在一最佳解O,那麼我們會希望求解出來的A=O,但是我們又無法保證此問題僅有一最佳解的集合,且我們的要求是要求 完成最多數量的requests,因此我們僅須證明|A|=|O|,也就是兩集合包含相同數量即可。
接下來如同標題所寫,我們以"Stay ahead"來證明,也就是說A至少或優於O。比較貪婪演算法建構起來的部分A是否優於O的部分,且每一步都是優於O的。
符號定義
s(i) 為requests i 的起始時間
f(i) 為requests i 的結束時間
R 所有可被選擇的requests集合
A={i1, ...., ik } 演算法產生的集合A包含k個被接受的requests,且i照時間上升排序。
O={j1, ... , jm} 最佳解集合O包含m個被接受的requests,且j照時間上升排序。
定理2
對於所有註標r ≤ k,f(ir) ≤ f(jr)
這一定理是為了符合我們所說 集合A stays ahead O,所以f(ir)至少會小於等於 f(jr)。
證明

以歸納法證明,在r=1時,此定理必然為真,因為演算法會挑出最早結束的時間(f(ir)最小的i)。
現在證明r>1的部分,我們歸納假設 "此定理在r-1時仍為真",並試著證明在r時也成立。以上述假設我們可以說f(ir-1) ≤ f(jr-1),見上圖,但是否會出現在f(ir) > f(jr)的情形呢?不,因為如上圖所示,演算法永遠有機會選擇jr(較早結束),以滿足我們的假設。
又因為O為最佳解,代表裡面的requests必然不衝突,因此得到f(jr-1) ≤ s(jr),而f(ir-1) ≤ f(jr-1),所以 f(ir-1) ≤s(jr),代表在選擇完ir-1要選擇下一個request時,我們可以選擇jr(jr在集合R當中),而該演算法會挑選最早完成的,因此可以知道f(ir) 至少小於等於 f(jr),完成歸納步驟。
因此目前我們可以確定貪婪演算法在每一個r中,保持優於最佳解O,因為定理2所述,A當中每個選擇都至少小於等於O。
定理3
此貪婪演算法回傳一最佳解集合A
證明
以反證法證明,若A並非最佳解,那麼O必然有多出一個request,也就是說m>k。使用定理2,當r=k時,我們有f(ik) ≤ f(jk),而m>k,代表O存在jk+1,此request在jk結束後開始(當然也必然在ik之後)。代表在我們挑選完i1, ..., ik並刪除集合R當中與之衝突的requests時,仍剩下一個request jk+1,但是此貪婪演算法的終止條件是R為空集合,產生矛盾。
實行與執行時間
1.Initially let R be the set of all requests, and let the set of accepted requests A be 2.empty
3.While R is not yet empty
4. Choose a request i∈R that has the smallest finishing time
5. Add request i to A
6. Delete all requests from R that are not compatible with request i
7.EndWhile
8.Return the set A as the set of accepted requests
演算法時間複雜度為O(nlogn),主要有以下步驟
- 將集合R當中的元素依升冪排序 (排序最快為O(nlogn))
- 紀錄開始時間,陣列S, S[i]=s(i) (O(n))
- while迴圈會掃描一遍集合R (O(n))
Stays Ahead - Interval Partition
也稱為Interval Coloring Problem,算是上一節
的一種,這次是要以最少的資源去完成所有工作
Given : 一堆附有起始、結束時間的工作集合(set of jobs with start times and finish times)
Goal :將這些request分割成數個(追求最少個數)相容的子集合,每個集合會分配到一資源。
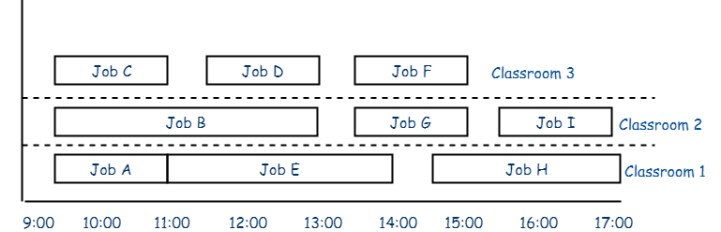
定理1
至少需要和interval集合深度(depth)一樣多的資源。
*以上圖為例,depth就是3。
考慮兩個問題
- 是否能發展一演算法排完所有的requests且使用最少的資源
- 真的都存在一schedule使用最少的資源(資源數等於其depth)
設計演算法
Sort the intervals by their start times, breaking ties arbitrarily
Let I1,I2,...,Ik denote the intervals in this order
For j=1,2,3,...,k
For each interval Ii that precedes Ij in the sorted order and overlaps it
Exclude the label of Ii from consideration for Ij
EndFor
If there is any label from {1,2,...,d} that has not been excluded then
Assign a nonexcluded label to Ij
Else
Leave Ij unlabeled
EndIf
EndFor
An exchange argument - Scheduling to minimize lateness
可以用交作業的概念來解釋。不過目標是有最少的遲交時間,通常現實生活只要遲交就是不行:(
Given: a single resource is available. A set of requests {1, 2, ..., n}, ith request requires time of length ti and has deadline di
Goal: schedule all requests without overlapping to minimize the maximum lateness
Lateness: li = max{0, fi -di }
Greedy Rule
找所需時間最短的
反例:做完1在做2會讓2遲交,但其實可以兩個都不。
任務 1 2 t(完成所需天數) 1 10 d(距離截止日期天數) 100 10 smallest slack(也就是d-t最小)
反例:先做2,會讓1的延遲大幅提升。
任務 1 2 t(完成所需天數) 1 10 d(距離截止日期天數) 2 10 找截止時間最近的
暫時找不到,所以要來證明,雖然乍看之下,他完全不考慮任務執行所需時間有點不合理。
Pseudo Code
Interval-partitioning(n,t1,..,tn,d1,..,dn)
Setup t=0 and sort requests so that d1<=...<=dn
For j=1 to n
assign request j to time interval [t,t+tj]
sj=t,fj=t+tj
t=t+tj
定理1
存在一最佳排程,其不含idle time
*idle time指的是有時間沒有排工作。
因為先做deadline最近的,所以做完後一定有其他工作可以做。
我們求出來的解稱為A,而問題本身存在一最佳解O,目標是將O逐步改為A,但過程中確保依舊保持最佳解。
定理2
所有沒有inversion和idle time的排程都含有相同的最大延遲時間
*inversion指的是截止日較晚的工作i被排在截止日較近的工作j之前。
定理3
存在一最佳解,沒有inversion和idle time
證明
從一不含idle time的最佳解開始,
- 如果O有inversion,那麼存在一排程{i,j},但di>dj
假設O至少有一個inversion,且如上所假設是工作i,j,我們將ij交換,減少inversion,且不會增加新的inversion。
- 在交換ij後,得到少了一組inversion的O
最難的部分就是要證明交換後的O仍是optimal,也就是下面這點
- 新的排程所擁有的最大延遲不會大於原本的排程
原先的排程至多可以有n取2個inversion,也就是至多n取2個交換就可以得到沒有inversion的最佳解。因此我們就是希望證明交換一對又一對的工作時,不會增加最大延遲。
用一些符號表是最佳排程O
每一個request r配安排在時間區間[s(r),f(r)],且其延遲時間為lr',L' = max(lr')。
原本的工作是i,j,且di>dj,用f、l表示。將ij交換,變成j,i並以f'和l'表示。
l'(i) = f'(i)-d(i), f'(i)-d(i) 又等於f(j)-d(i),
且dj<di,所以
l'(i) =f(j)-d(i) < f(j) - d(j)=l(j)
由上面等式可以知道I'(i) < l(j),也就是交換後並不會增加最大延遲時間。
演算法產生的排程A會有最佳的最大延遲時間。